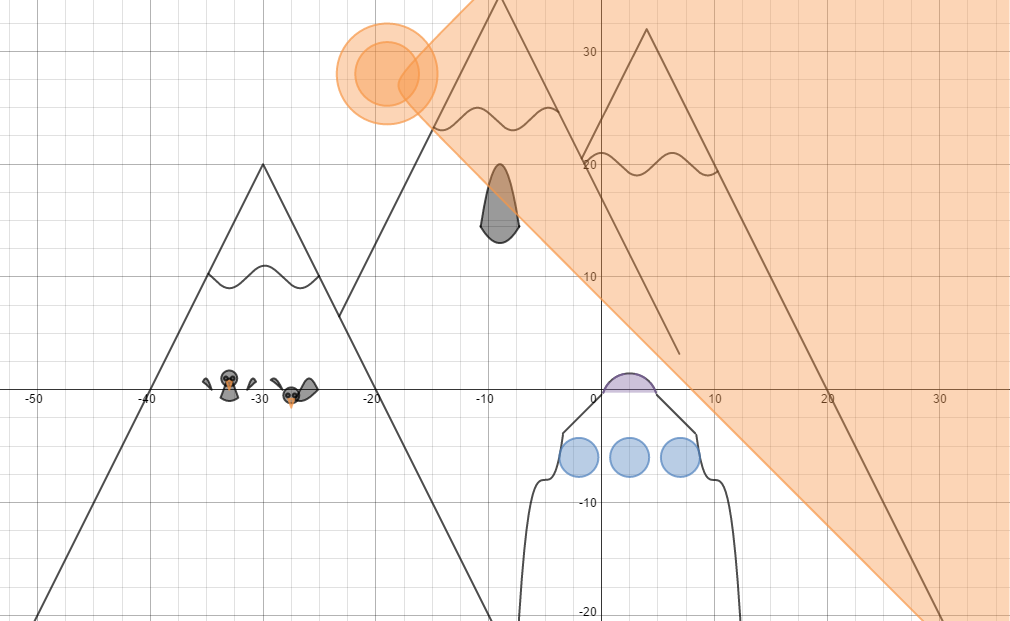
Unit 4 - Desmos Drawing Project with Function Families
Annotations:
- Most of the mountains are made up the absolute value function, y=a丨x-h丨+k .
- For one of the mountains I used two linear equation, y=mx+b.
- All the circles are constructed using the equation (x-h)2+(y-k)2=r.
- The penguin bodies are from the equation sin ax>y>sin x, which is a type of inequality.
- All the circles are made up of the equation (x-h)2+(y-k)2=r. h and k being the center of the circle and where it is located.
- The beaks of the penguins are made by the equation y=a丨x-h丨+k.
- The sunshine is (x-h)2-(y-k)2=r, which is - instead of being a circle which is +.
- The tower thing is made of a half a circle at the top and three other circles. The sides are parent functions. y=a(x-h)3+k.
Reflection:
To go about drawing my art using only equations was not so mathematical at first. I started by thinking about what I was going to draw and then completely changing it. I was going to create a rollercoaster because it would be the ‘easiest’ thing to do while still using all the equations but it was too boring, both creating and the theme. I thought it was to granola so I decided to change it to a bunch of mountains. Then after that a bunch of snowy mountains with a cave and penguins on it, later to be called Penguin Party. For most of the equations I simply went by the examples except for the penguins. For the penguin bodies I used equations that involved sine and cosine and > and <.
Using Desmos to graph actually really helped me understand the equations a lot more than I did before. For example, before I knew how a circle could be constructed but not what the variables really meant. I knew that each variable had to mean something but not what that something did. I plugged in 0 for h (moved left or right)or k (moved up or down) and 1 for r (size of circle), not really knowing what it would do on the graph. Through graphing on Desmos I now have a better understanding of h and k and how changing r could change the circle size so much or so little. Another function family I learned more about is y=x^2 added a, h, or k. I was able to easily visualize how this function works in that due to x being squared y will always be positive. Y will always be positive because a negative multiplied by a negative is always a positive.
Using Desmos to graph actually really helped me understand the equations a lot more than I did before. For example, before I knew how a circle could be constructed but not what the variables really meant. I knew that each variable had to mean something but not what that something did. I plugged in 0 for h (moved left or right)or k (moved up or down) and 1 for r (size of circle), not really knowing what it would do on the graph. Through graphing on Desmos I now have a better understanding of h and k and how changing r could change the circle size so much or so little. Another function family I learned more about is y=x^2 added a, h, or k. I was able to easily visualize how this function works in that due to x being squared y will always be positive. Y will always be positive because a negative multiplied by a negative is always a positive.
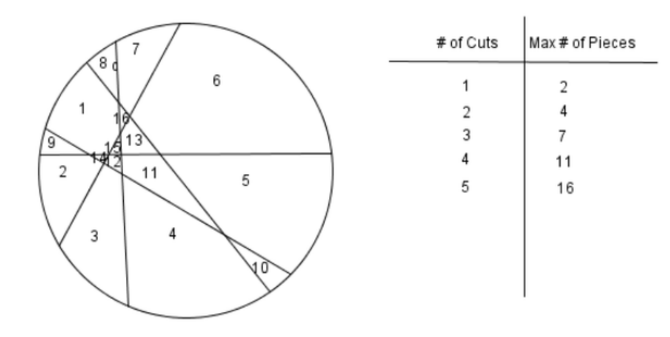
Pow #1: Slices of Pie
For this POW we were asked the question of how many pieces could you get with 1 straight slice that slices through the whole pie? With 2 slices? With 3 slices? With 4 slices? With 5 slices? What I found out is that to get the max amount of pieces each slice has to intersect with each other. Also that there is a pattern, the previous max amount of pieces added to the number of cuts gives the max number of pieces for the cuts. The best way to say that mathematically is f(x)= .5x^2+.5x+1, x being the number of cuts. Using this equation/pattern I can say the max number of pieces from 10 cuts would be 56 pieces. This pattern is occurring because each cut added if placed correctly can intercept the other cuts creating even more pieces out of just a few, and so on.
Some extensions that could have made this much more difficult and interesting is the rule that each cut must turn at a 90 degree angle at some point. This would make this much more challenging but might not give a clear output. Another problem could even just be using another more interesting shape, such as a star shape. My personal reaction to this is I actually enjoyed this POW because I was able to learn the content in a more fun way. From this POW I learned how to make a different type of equation and how to translate the seen pattern into a function. I enjoyed this POW much more than the others and I thought it was a little on the easy side. For this POW I would give myself a 23 out of 25 because I did really well on it and was thorough, but I was given extra time because I forgot to check the rubric the first time.
Steps:
Construct circle.
Use straight edge to create first line wherever.
Create a line that goes that bisects the all other lines but does not bisect two or more lines at one point.
Repeat last step.
Some extensions that could have made this much more difficult and interesting is the rule that each cut must turn at a 90 degree angle at some point. This would make this much more challenging but might not give a clear output. Another problem could even just be using another more interesting shape, such as a star shape. My personal reaction to this is I actually enjoyed this POW because I was able to learn the content in a more fun way. From this POW I learned how to make a different type of equation and how to translate the seen pattern into a function. I enjoyed this POW much more than the others and I thought it was a little on the easy side. For this POW I would give myself a 23 out of 25 because I did really well on it and was thorough, but I was given extra time because I forgot to check the rubric the first time.
Steps:
Construct circle.
Use straight edge to create first line wherever.
Create a line that goes that bisects the all other lines but does not bisect two or more lines at one point.
Repeat last step.
POW #2
For this POW we were asked a question about how you many pairs of similar triangles we could make. The supplies we were given was four rods, 6, 4, 3, and 2 inches long. Along with that two more rods from the extra supply that could range from 1 to 20 inches long. To even try to create a pair you would have to use all the rods provided to do it correctly. You can only make one pair at a time and one triangle must be a copy of the original but does not have to be the same size. The first thing I did to begin to understand the problem is look for rod lengths that all multiply to another rod length by 2. Some key insights that is important in understanding the problem is knowing how to connect the lines because if you draw these triangles you're going to need a compass. Also it is important that you know how similar triangles are similar because otherwise you will not understand the question asked. How I organized my information and results is just by having the triangles created on a piece of paper with the measurement on the sides. To find all the triangle I actually did not use any patterns. All I needed to know for this problem is simple Algebra. Similarity means that they are the same shape and can be smaller or larger. I know the triangles I made were similar because one could fit in the other one like this:
The side lengths that could form a triangle were 6, 4, 4, and 3, 2, 2, and 5, 4, 2, and finally 6, 5, 3. The triangles that were similar were 6, 4, 4, and 3, 2, 2, along with 5, 4, 2, and 6, 5, 3. Two pairs was the most amount of similar triangles I could make. Some variations to the problem could simply changing out the rods for new ones and maybe more rods. I thought this POW was not very difficult but time consuming. I learned from this POW that creating similar triangles can be easy if I put time into it. I would give myself a 24 out of 25 because I put the effort needed into it and I went back and refined it to make sure to get a high score.
The side lengths that could form a triangle were 6, 4, 4, and 3, 2, 2, and 5, 4, 2, and finally 6, 5, 3. The triangles that were similar were 6, 4, 4, and 3, 2, 2, along with 5, 4, 2, and 6, 5, 3. Two pairs was the most amount of similar triangles I could make. Some variations to the problem could simply changing out the rods for new ones and maybe more rods. I thought this POW was not very difficult but time consuming. I learned from this POW that creating similar triangles can be easy if I put time into it. I would give myself a 24 out of 25 because I put the effort needed into it and I went back and refined it to make sure to get a high score.
POW #4
The problem for this POW involved a 5 by 5 by 5 cube, more specifically 125 small cubes and a N by N by N cube for an extra challenge. The problem that was asked of the students to address was counting the number of smaller cubes that were in a 5 by 5 cube. We had to assume that the 5 by 5 cube was painted only on the outside and count the smaller cubes that were painted and unpainted. We counted the number of smaller cubes with 1 face, 2 faces, 3 faces, 0 faces, and 4, 5, and 6 faces painted. How I went about counting the cubes for the 5x5x5 is actually not as simple as you might think. Because the outer edged smaller cubes are part of one or two faces you can’t just multiply one side by 6. You must take into count the cubes that are on the edges that have multiple sides painted and also the ones that only have one side painted the are not on the edges but are still on the surface. Also that the corner cubes have three faces painted and there is a 3x3x3 of cubes in the center unpainted. What helped me count the cubes with one face painted was knowing that there was a 3x3 on one side of the larger cube and since a cube has 6 sides it is a simple equation, (3x3)6. I also found that the smaller cubes with one face painted were the number per one side of the larger square multiplied by the number of edges on the larger square as well, 12x3. The last one is the smaller cubes with 3 faces painted, because there are only 3 face painted cubes on all 8 corner of the larger cube there are only 8.
What was found using this process was that there are 54 cubes with one face painted, 36 two faces painted, and 8 three faces painted, adding up to 98. 98 Meaning that there are 27 cubes unpainted making up a 3x3x3 of unpainted cubes in the center. However, there are no cubes that can have 4, 5, or 6 faces painted due to the fact that there are only six sides to one whole cube, with the exception of a 1x1x1 cube. A problem that is similar to this one is there is a 5x5x8 rectangle that is hollow after one layer of 1x1x1 cubes and only the inside of the box is painted. How many cubes are painted? This POW made me think at a larger scale of things. Instead of a 5x5 it was a 5x5x5 that had layers as well. It helped me realize how a cube is much more unique than a flat square, especially when it is made of smaller cubes.
What was found using this process was that there are 54 cubes with one face painted, 36 two faces painted, and 8 three faces painted, adding up to 98. 98 Meaning that there are 27 cubes unpainted making up a 3x3x3 of unpainted cubes in the center. However, there are no cubes that can have 4, 5, or 6 faces painted due to the fact that there are only six sides to one whole cube, with the exception of a 1x1x1 cube. A problem that is similar to this one is there is a 5x5x8 rectangle that is hollow after one layer of 1x1x1 cubes and only the inside of the box is painted. How many cubes are painted? This POW made me think at a larger scale of things. Instead of a 5x5 it was a 5x5x5 that had layers as well. It helped me realize how a cube is much more unique than a flat square, especially when it is made of smaller cubes.
POW #5 The Ideal Soda Can
The problem for this POW was based on the volume of a soda can. The problem was how to use the least amount of resources per can of 12 ounces or a volume of 355 mls or 355 cm3. To find this out we were able to change the radius and height, one dependent on the other to ensure the same volume of a 12 ounce can. My process that I took was basically to test two numbers, high and low. For example 2 and 5. The way I thought about this problem was that if I could take educated guesses that I will be able to easily keep track of the lowest and at the same time decrease the amount of work I had to do. I used these numbers for two different cans’ radius’ and after chose a number somewhere in the middle. When I finished that part I did one more number between the numbers with the lowest amount of Surface Area (SA). From there I reviewed all the answers and I made another can diagram using the two smallest ones with the lowest amount of SA to pinpoint the next lowest, then repeated until it was certain I found the smallest amount of SA. Since I used the radius as an independent variable I used the equation that allows me to find the height of the can, r2355=h. Pi multiplied by the radius squared then divided by the volume, 355 cm cubed. To find the Surface Area you have to find the circumference of the cylinder so that you know the width of the rectangle that is making it a cylinder. After that you multiply the circumference by the height (ch) then add it to the area of both circles on the top and bottom (2r2). In the end I organized my data by putting !’s on the can with the lowest SA and the amount of !’s represented how low it is. The lowest one had two !’s, meaning it was the second one I found.
The solution that I came up with is a soda can that has a Surface Area of 277.57 cm squared, a radius of 3.9 cm, and a height of 7.433 cm. I think this is the lowest amount of SA possible because if the radius is changed whatsoever the SA will increase. Also the radius and height does not correspond to the size of a current 12 ounce soda can. I think that the current soda can dimensions are being used for not saving resources but instead making the shape more appealing to the eye. For this problem we disregarded the shape but focused on saving resources. We did not focus on how visually appealing the can is which can actually increase profits. In the end making it well worth it to lose some resources in the making of each can, such as aluminum. This POW made me think differently in that I had to do many trials to find the best solution. It also made me practice educated guessing which can be quite useful.
The solution that I came up with is a soda can that has a Surface Area of 277.57 cm squared, a radius of 3.9 cm, and a height of 7.433 cm. I think this is the lowest amount of SA possible because if the radius is changed whatsoever the SA will increase. Also the radius and height does not correspond to the size of a current 12 ounce soda can. I think that the current soda can dimensions are being used for not saving resources but instead making the shape more appealing to the eye. For this problem we disregarded the shape but focused on saving resources. We did not focus on how visually appealing the can is which can actually increase profits. In the end making it well worth it to lose some resources in the making of each can, such as aluminum. This POW made me think differently in that I had to do many trials to find the best solution. It also made me practice educated guessing which can be quite useful.
Steps:
Construct circle.
Use straight edge to create first line wherever.
Create a line that goes that bisects the all other lines but does not bisect two or more lines at one point.
Repeat last step.
Construct circle.
Use straight edge to create first line wherever.
Create a line that goes that bisects the all other lines but does not bisect two or more lines at one point.
Repeat last step.
POW #1:
|
The problem for this POW is on a 3x3 there are two black knights and two white knights that need to switch places in as few moves. The problem is that knights can only move in a L shape. To keep track of each move I tallied each move. I have tried all the ways I know and there seems to be only one minimal answer. The answer that has the least moves is 15 moves.
|
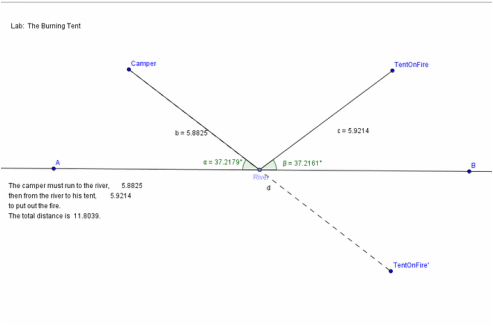
The Burning Tent Geogebra Lab:
Questions:
Question 1: Once you have a minimal path, what appears to be true about the incoming angle and the outgoing angle?
The incoming angle and outgoing angle are basically congruent.
Question 2: Why is the path from points Camper to TentFire' the shortest path? Briefly explain. (Think about the shortest distance between two points.)
This is the shortest path because the angles are congruent because one side of the path is basically mirrored to create the other side. Also both angles are as small as possible without making the other angle larger.
Question 3: Where should the point River be located in relation to segment Camper to TentFire' and line AB so that the sum of the distances is minimized?
Point River should be located at the middle of where a perpendicular line would be put on line ab. Also on the line of reflection for the path.
The incoming angle and outgoing angle are basically congruent.
Question 2: Why is the path from points Camper to TentFire' the shortest path? Briefly explain. (Think about the shortest distance between two points.)
This is the shortest path because the angles are congruent because one side of the path is basically mirrored to create the other side. Also both angles are as small as possible without making the other angle larger.
Question 3: Where should the point River be located in relation to segment Camper to TentFire' and line AB so that the sum of the distances is minimized?
Point River should be located at the middle of where a perpendicular line would be put on line ab. Also on the line of reflection for the path.
Tessellation Project
The theme of my tessellation is Elephants on trees. I started with a square and translated two sides to their opposite side. Tessellations are Art because there is beauty in them. Also because it is a drawing that is based on creativity.
Instructions on how I made my Tessellation:

1. Start with a square and sketch your image.
2. Cut out what would be translated to the opposite side.
3. Line up the pieces that were cut out on the other side.
4. Then tape them to the side of the squares.
2. Cut out what would be translated to the opposite side.
3. Line up the pieces that were cut out on the other side.
4. Then tape them to the side of the squares.
"I think a figure is symmetric when a line can divide the figure into two congruent halves. A butterfly is an example. If I draw a line down the center of the butteryfly's body, each half of the butterfly looks the same, like a mirror reflection." -Student at http://www.shodor.org/interactivate/discussions/SymmetryInTessellati/
A tessellation possesses translational symmetry if it can be translated by some vector and remain unchanged. Any tessellation with this property has inifinitely many different translation vectors due to the infinite extent of tessellations. The tessellation below has translational symmetry; two possible vectors are shown. Find additional vectors. (http://mathartfun.com/shopsite_sc/store/html/Tessellations/SymmetryTess.html)
A tessellation possesses translational symmetry if it can be translated by some vector and remain unchanged. Any tessellation with this property has inifinitely many different translation vectors due to the infinite extent of tessellations. The tessellation below has translational symmetry; two possible vectors are shown. Find additional vectors. (http://mathartfun.com/shopsite_sc/store/html/Tessellations/SymmetryTess.html)
Snail Trail Lab:
In creating this I constructed a circle. Then after I divided the circle in six parts and put a point in one of the areas. Then I reflected the point on all the equal parts throughout the circle to create the snails. After, I made it so all the snails left a trail of the color they are where ever they were dragged. When one was dragged all of them followed because they were constantly reflecting each other. This lab has reflectional symmetry and rotational symmetry of 120 degrees. During this project I had fun and learned some new things in Geogebra. I also learned how lines of reflection work.